Les spirales comptent

L’émergence de la morphologie galactique et des lois d’échelle

Résumé

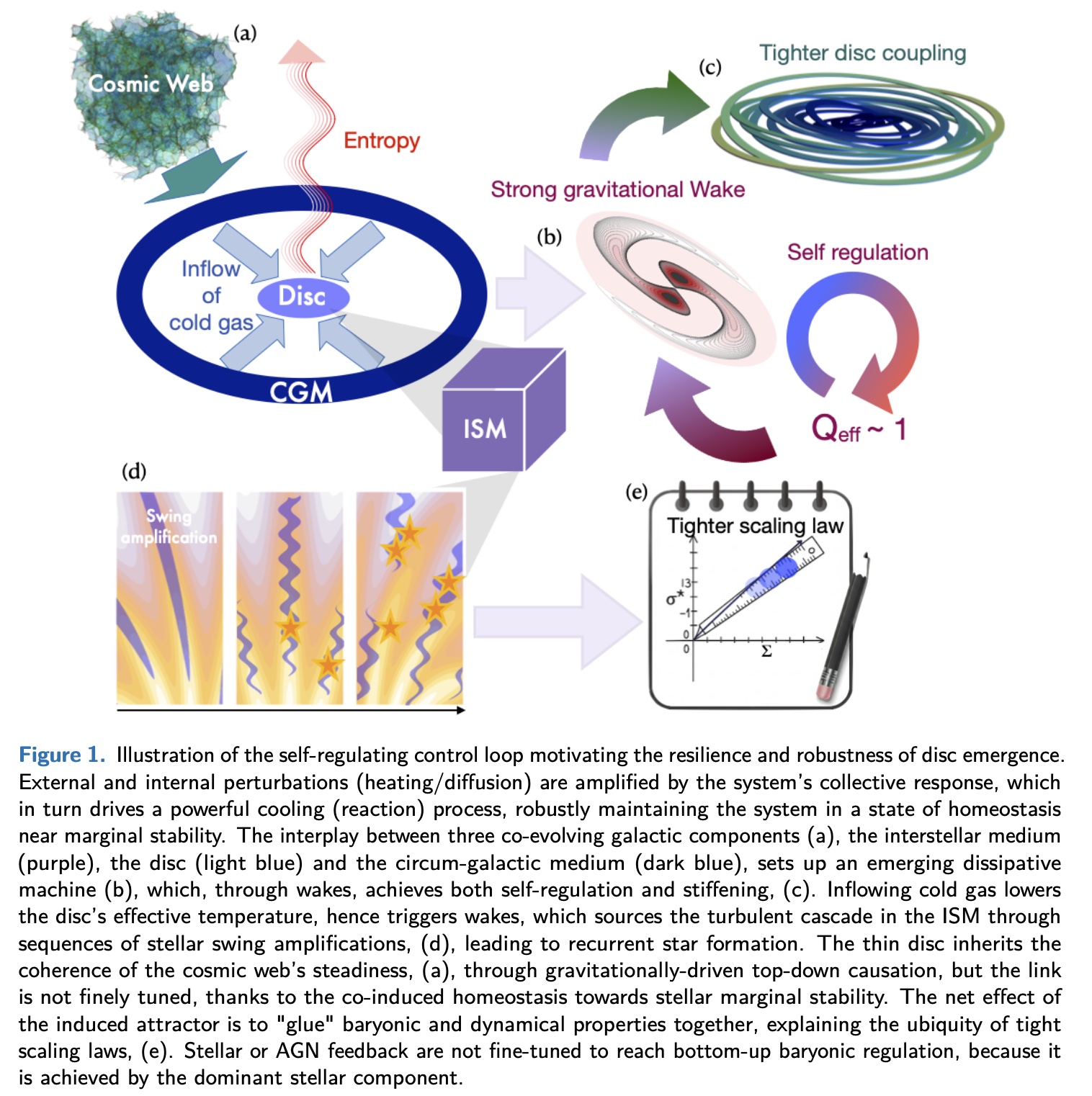
Les disques galactiques minces sont désormais observés sur toute l’histoire cosmique avec JWST, y compris à des époques où les scénarios hiérarchiques standards de formation prédisent de fortes perturbations. Leur survie à long terme ne peut pas s’expliquer uniquement par la conservation du moment angulaire ni par un ajustement fin de rétroactions à petite échelle. Leur résilience semble au contraire provenir d’un mécanisme robuste d’auto-régulation gravitationnelle : les perturbations qui chauffent le disque déclenchent une réponse gravitationnelle collective qui, combinée à l’apport de gaz froid, ramène le système vers un état de stabilité marginale. Cette interaction agit comme une puissante boucle homéostatique, rigidifiant le disque et resserrant des lois d’échelle telles que Tully–Fisher, la relation d’accélération radiale, ainsi que les corrélations entre formation stellaire, métallicité et cinématique. Lorsque cette boucle échoue, des perturbations rares peuvent induire des transitions non locales (de type instanton) vers des galaxies barrées, qui correspondent à un autre attracteur.

Cette thèse de doctorat explorera comment les galaxies à disque fonctionnent comme des structures dissipatives émergentes et auto-organisées, et pourquoi leurs propriétés présentent un ordre aussi remarquable.

Contexte astrophysique

La persistance des disques minces et de leurs lois d’échelle très serrées est centrale pour la cosmologie de précision, car des relevés tels qu’Euclid et LSST reposent fortement sur la morphologie des galaxies. Un paradoxe ancien demeure non résolu : dans le cadre de ΛCDM, les galaxies évoluent dans un environnement perturbé, avec des apports continus et des interactions de satellites, alors que les observations révèlent des disques structurellement fragiles mais étonnamment durables. JWST a renforcé cette tension en montrant que de tels disques existent déjà à grand redshift. Cette thèse testera si une forme d’auto-régulation « top-down », pilotée par les spirales, permet de résoudre ce paradoxe. L’hypothèse est qu’une réponse gravitationnelle multi-échelle, l’inflow de gaz et une formation stellaire turbulente mettent en place une boucle de rétroaction auto-organisée maintenant les disques près de la stabilité marginale. Cette boucle explique simultanément leur résilience et l’émergence de lois d’échelle serrées : le désordre interne induit par les perturbations est contrebalancé par des processus de « refroidissement » alimentés par le gaz froid, qui reconstruisent des orbites ordonnées. L’attracteur résultant relie étroitement les propriétés baryoniques (formation stellaire, fraction de gaz, métallicité) aux propriétés dynamiques (masse du halo, distribution du moment angulaire), réduisant la dispersion intrinsèque : les spirales comptent ! Comprendre ce comportement homéostatique est crucial pour interpréter les biais dépendant de la morphologie dans les inférences cosmologiques.

Méthode

Deux avancées récentes permettent désormais de modéliser l’évolution des disques de manière perturbative plutôt que de s’appuyer sur des simulations coûteuses : i) la validation de formalismes issus de la théorie cinétique décrivant l’échauffement des disques par diffusion orbitale ; ii) de nouveaux développements en théorie des grandes déviations décrivant les fluctuations et la diversité morphologique au-delà de l’évolution de champ moyen. La thèse étendra ces outils afin de formuler une équation réaction–diffusion quasi-linéaire dissipative et auto-cohérente (« habillée ») pour les disques galactiques. Le terme de diffusion décrira l’échauffement gravitationnel stochastique induit par des fluctuations internes et externes. Le terme de réaction décrira le refroidissement fourni par l’apport de gaz froid et la formation d’étoiles sur des orbites ordonnées. La réponse gravitationnelle collective (« habillage ») encodera l’amplification résonante des spirales et déterminera comment les perturbations sont amplifiées ou supprimées en fonction de l’état du disque.

L’étudiant·e explorera les solutions stationnaires, les bifurcations et les seuils de survie ou d’échec des disques, à l’aide de modèles perturbatifs et d’expériences numériques ciblées. Le formalisme sera confronté aux données de relevés (JWST, Euclid, LSST, DESI) afin de quantifier la résilience dépendante de l’environnement et son empreinte sur la dispersion des lois d’échelle. À l’issue de la thèse, l’étudiant·e aura démontré comment la gravité assure une causalité top-down à travers les échelles — des apports du réseau cosmique à la turbulence du milieu interstellaire — et pourquoi les disques minces restent cohérents pendant des milliards d’années. Il ou elle quantifiera également les biais induits dans les mesures cosmologiques et proposera des méthodes pour les marginaliser.

Objectifs scientifiques spécifiques

L’étudiant·e en thèse cherchera à :

  • Démontrer comment des processus baryoniques pilotés par la gravité établissent une boucle d’auto-régulation maintenant la stabilité marginale des disques et resserrant les lois d’échelle galactiques.
  • Développer des modèles dissipatifs de théorie cinétique ouverte (réaction–diffusion, grandes déviations) pour suivre l’amincissement des disques et leur résilience sur des temps séculaires.
  • Prédire des observables (épaisseur des disques, fraction barres/bulbes, dispersion des lois d’échelle (bTF/RAR/KS/métallicité–cinématique)) en fonction de l’environnement et du redshift, en vue de comparaisons avec les instruments actuels et futurs.
  • Identifier des seuils dépendant de l’environnement où l’auto-régulation échoue, menant à l’extinction séculaire ou à la formation de barres, ou au contraire où elle persiste, menant à des super-spirales.
  • Quantifier les biais induits par la morphologie dans les relevés cosmologiques et proposer des corrections physiquement motivées.

Pré-requis

Fort intérêt pour l’astrophysique théorique, la dynamique galactique, la modélisation analytique et l’expérimentation numérique.

Encadrement

La thèse sera co-encadrée par Christophe Pichon, Damien Le Borgne (IAP, Paris), Philippe Salomé (Observatoire de Paris) et Maxime Trebitsch (Observatoire de Paris), dans le cadre de l’ANR GALBAR (https://www.secular-bars.org).

Références

  • Thèses d’anciens étudiants disponibles ici
  • Binney, J., & Lacey, C. 1988 MNRAS, 230 (4), 597–627
  • Bournaud, F., et al. 2007, ApJ, 670, 237
  • Domez T., et al. 2023, MNRAS, 527, 2139
  • Fouvry, J.-B., et al. 2015, A&A, 584, A129
  • Fouvry, J.-B., et al. 2015, MNRAS, 449, 1967
  • Fouvry, J.-B., et al. 2015, MNRAS, 449, 1982
  • Fouvry, J.-B., et al. 2017, MNRAS, 471, 2642
  • Fouvry, J.-B., et al. 2021, MNRAS, 508, 2210
  • Feliachi O, et al. 2022 Stat.186
  • Hopkins, P. F., et al. 2014, MNRAS, 445, 581
  • Julian, W. H., & Toomre, A. 1966, ApJ, 146, 810
  • Kormendy, J., & Kennicutt, R. C. Jr. 2004, ARA&A, 42, 603
  • Kraljic, K., et al. 2018, MNRAS, 474, 547
  • Kraljic, K., et al. 2020, MNRAS, 493, 362
  • Vega-Ferrero, J. et al 2024 ApJ 961 51
  • Lelli, F., et al. 2019, MNRAS, 484, 3267
  • Leroy, A. K., et al. 2008, AJ, 136, 2782
  • Lian, J., & Luo, L. 2024, ApJL, 960, L8
  • McGaugh, S. S. 2012, AJ, 143, 40
  • Michikoshi, S., & Kokubo, E. 2016, ApJ, 821, 35
  • Papastergis, E., et al. 2016, A&A, 593, A39
  • Park, M., et al. 2021, MNRAS, 530, 4378
  • Pichon, C., Aubert, D. 2006 MNRAS, v368, 1657-1694
  • Pogosyan, D., et al. 2009, MNRAS, 396, 635
  • Ristea, A., et al. 2024, MNRAS, 527, 7438
  • Robertson, B., et al. 2006, ApJ, 645, 986
  • Romeo, A. B., et al. 2010, MNRAS, 407, 1223
  • Roule, M., et al. 2022, PRE, 106, 044118
  • Roule, M., et al. 2025, A&A, 699, A140
  • Rozier, S., et al. 2019, MNRAS, 487, 711
  • Sellwood, J Carlberg, 1984 ApJ 282, 61
  • Tep, K., et al. 2022, MNRAS, 514, 875
  • Toomre, A. 1964, ApJ, 139, 1217
  • Tumlinson, J., Peeples, M., & Werk, J. K. 2017, ARA&A, 55, 389
  • Vogelsberger, M., et al. 2020, MNRAS, 492, 5167
  • Weinberg, M. ApJ, 2001, 328, 321