Spirals Matter

The emergence of Galactic Morphology and Scaling Laws

Upshot

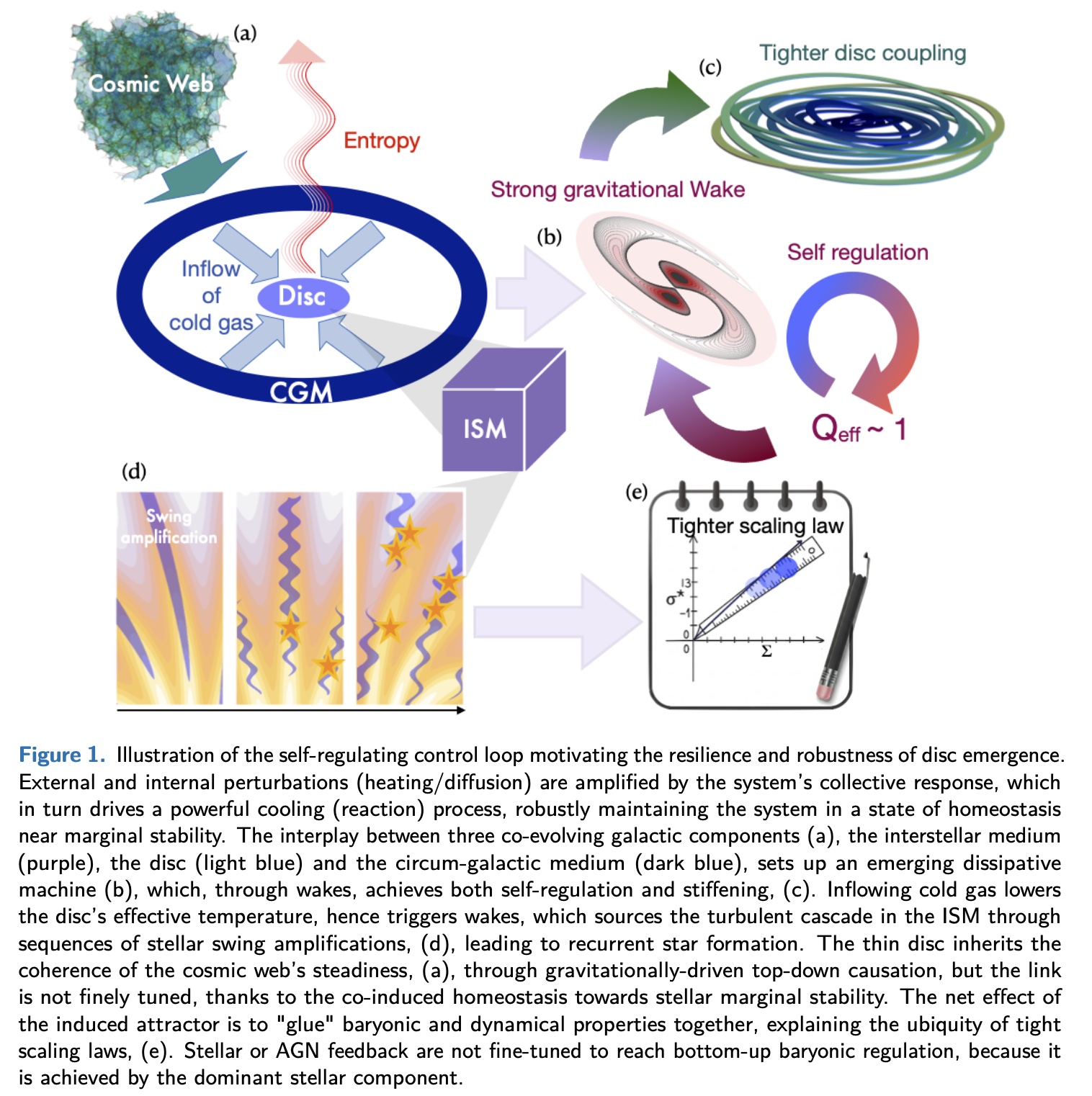
Thin galactic discs are now observed across cosmic time with JWST, including at epochs where standard hierarchical formation scenarios would predict strong perturbations. Their long-term survival cannot be explained solely through angular-momentum conservation or finely tuned small-scale feedback. Instead, their resilience appears to stem from a robust gravitational self-regulation mechanism: perturbations that heat the disc trigger a collective gravitational response which, together with cold gas inflow, drives the system back toward marginal stability. This interplay acts as a powerful homeostatic loop, stiffening the disc and tightening scaling relations such as Tully–Fisher, the radial-acceleration relation, and star-formation–metallicity–kinematics correlations. When the loop fails, rare event perturbations can drive non local (instanton-like) transition to barred galaxies, which correspond to another attractor.

This PhD will explore how disc galaxies function as emergent, self-organised dissipative structures, and why their properties display such remarkable order.

Astrophysical Context

The persistence of thin discs and their tight scaling laws is central to precision cosmology, since surveys such as Euclid and LSST rely heavily on galaxy morphology. A long-standing paradox remains unresolved: in ΛCDM, galaxies evolve within a perturbed environment with continuous inflow and satellite interactions, yet observations reveal structurally fragile but long-lived discs. JWST has strengthened this tension by showing that such discs already exist at high redshift. This PhD will test whether a top-down, spiral-driven form of self-regulation resolves this paradox. The hypothesis is that multi-scale gravitational response, gas inflow, and turbulent star formation set up a self-organised feedback loop that maintains discs near marginal stability. This loop simultaneously explains their resilience and the emergence of tight scaling laws: internal disorder induced by perturbations is counterbalanced by cold-gas-driven “cooling” processes that rebuild ordered orbits. The resulting attractor glues baryonic properties (star formation, gas fraction, metallicity) to dynamical ones (halo mass, angular momentum distribution), reducing intrinsic scatter: spirals matter! Understanding this homeostatic behaviour is crucial for interpreting morphology-dependent biases in cosmological inference.

Method

Two recent advances now make it possible to model disc evolution perturbatively rather than relying on expensive simulations: i) the validation of kinetic-theory formalisms capturing disc heating through orbital diffusion; ii) new developments in large deviation theory describing fluctuations and morphological diversity beyond mean-field evolution. The PhD will extend these tools to formulate a dissipative, self-consistent quasi-linear ("dressed") reaction–diffusion equation for galactic discs. The diffusion term will capture stochastic gravitational heating driven by internal and external fluctuations. The reaction term will describe the cooling supplied by cold gas inflow and the formation of stars on ordered orbits. The collective gravitational response ("dressing") will encode spiral swing amplification and determine how perturbations are boosted or suppressed depending on the disc’s state.

The student will explore stationary solutions, bifurcations, and thresholds for disc survival or failure, using perturbative models and targeted numerical experiments. The formalism will be confronted with survey data (JWST, Euclid, LSST, DESI) to quantify environment-dependent resilience and its imprint on scaling-law scatter. When completed, the student will have demonstrated how gravity provides top-down causation across scales — from cosmic-web inflows to ISM turbulence — and why thin discs remain coherent over billions of years. They will also quantify the induced biases in cosmological measurements and propose ways to marginalize over them.

Specific scientific goals

The PhD student will aim to:

  • Demonstrate how gravity-driven baryonic processes establish a self-regulating loop that maintains disc marginal stability and tightens galactic scaling laws.
  • Develop dissipative, open kinetic-theory models (reaction–diffusion, large deviation) to follow disc thinning and resilience over secular timescales.
  • Predict observables (disc thickness, bar/bulge fraction, scatter in scaling relations (bTF/RAR/KS/metallicity-kinematics) as a function of environment and redshift, for comparison with current and upcoming facilities.
  • Identify environmentally driven thresholds where self-regulation fails, leading to secular quenching or bar formation, or conversely when it persists, leading to super spirals.
  • Quantify morphology-induced biases in cosmological surveys and provide physically motivated corrections.

Requirement

Strong interest in theoretical astrophysics, galactic dynamics, analytical modelling, and numerical experimentation.

Framework

The PhD will be co-supervised by Christophe Pichon , Damien Le Borgne (IAP, Paris), Philippe Salomé (Obs Paris) and Maxime Trebitsch (Obs, Paris) as part of the GALBAR ANR (https://www.secular-bars.org). Our established collaborations (20+ papers, over 3000 citations) will benefit from complementary synergies on ISM physics, super-spirals, observational, theoretical and numerical astrophysics.

References 

 PhDs of former students available  here.
  • Binney, J., & Lacey, C. 1988 MNRAS, 230 (4), 597–627
  • Bournaud, F., et al. 2007, ApJ, 670, 237
  • Domez T., et al. 2023, MNRAS, 527, 2139
  • Fouvry, J.-B., et al. 2015, A&A, 584, A129
  • Fouvry, J.-B., et al. 2015, MNRAS, 449, 1967
  • Fouvry, J.-B., et al. 2015, MNRAS, 449, 1982
  • Fouvry, J.-B., et al. 2017, MNRAS, 471, 2642
  • Fouvry, J.-B., et al. 2021, MNRAS, 508, 2210
  • Feliachi O, et al. 2022 Stat.186
  • Hopkins, P. F., et al. 2014, MNRAS, 445, 581
  • Julian, W. H., & Toomre, A. 1966, ApJ, 146, 810
  • Kormendy, J., & Kennicutt, R. C. Jr. 2004, ARA&A, 42, 603
  • Kraljic, K., et al. 2018, MNRAS, 474, 547
  • Kraljic, K., et al. 2020, MNRAS, 493, 362
  • Vega-Ferrero, J. et al 2024 ApJ 961 51
  • Lelli, F., et al. 2019, MNRAS, 484, 3267
  • Leroy, A. K., et al. 2008, AJ, 136, 2782
  • Lian, J., & Luo, L. 2024, ApJL, 960, L8
  • McGaugh, S. S. 2012, AJ, 143, 40
  • Michikoshi, S., & Kokubo, E. 2016, ApJ, 821, 35
  • Papastergis, E., et al. 2016, A&A, 593, A39
  • Park, M., et al. 2021, MNRAS, 530, 4378
  • Pichon, C., Aubert, D. 2006 MNRAS, v368, 1657-1694
  • Pogosyan, D., et al. 2009, MNRAS, 396, 635
  • Ristea, A., et al. 2024, MNRAS, 527, 7438
  • Robertson, B., et al. 2006, ApJ, 645, 986
  • Romeo, A. B., et al. 2010, MNRAS, 407, 1223
  • Roule, M., et al. 2022, PRE, 106, 044118
  • Roule, M., et al. 2025, A&A, 699, A140
  • Rozier, S., et al. 2019, MNRAS, 487, 711
  • Sellwood, J Carlberg, 1984 ApJ 282, 61
  • Tep, K., et al. 2022, MNRAS, 514, 875
  • Toomre, A. 1964, ApJ, 139, 1217
  • Tumlinson, J., Peeples, M., & Werk, J. K. 2017, ARA&A, 55, 389
  • Vogelsberger, M., et al. 2020, MNRAS, 492, 5167
  • Weinberg, M. ApJ, 2001, 328, 321