Secular Public

Secular-C: the vicinity of MBHs in a Hubble time

Compelling evidence for massive black holes (MBHs) exists for the nuclei of tens of nearby galaxies, including our own Milky Way (e.g. Genzel+’97). Scaling relations have been identified between MBHs and the large-scale properties of the host galaxy, such as mass, luminosity, and velocity dispersion (e.g. Heckman+’11). The energy pumped by Active Galactic Nuclei (AGN) into the host galaxy can energise the gas, suppressing star formation, thus altering the overall evolution of galactic structures (e.g. Springel+’05).

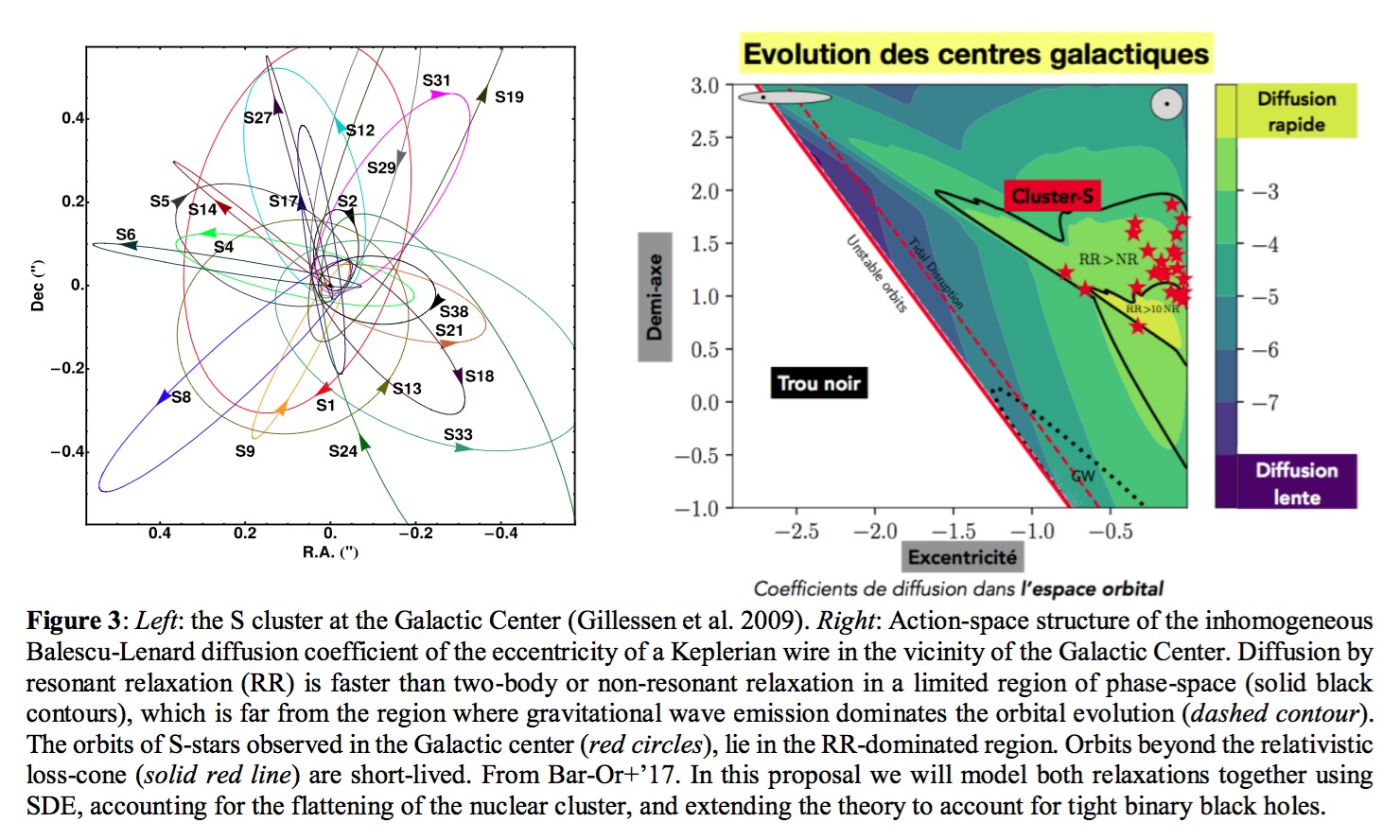
WPC1 Re-thinking the theory of nuclear star clusters The relationship between host galaxies and MBHs is critical to understanding galaxy evolution. In turn, its central stellar cluster holds the key to probing the MBH properties, such as their spin, their Schwarzschild Barrier or the expected extreme-mass-ratio-in-spirals (EMRI) rates. These stars evolve in a quasi-Keplerian potential hence their orbits take the form of ellipses, which conserve their spatial orientation for many orbital periods. They may therefore be represented as a system of massive Keplerian wires, for which the mass of each star is smeared out along the elliptic path followed by its quasi-Keplerian orbit. Such ideas were first developed in Rauch+’96, which introduced the concept of resonant relaxation by noting that wire-wire interactions greatly enhance the relaxation of the stars’ angular momentum (Alexander’05, Bar-Or+’17, Fouvry+19ab). These Keplerian wires can then undergo various effects on secular timescales: (i) vector resonant relaxation, during which a wire's orbital orientation gets to jitter stochastically through the non-spherical fluctuations in the cluster's potential, (ii) scalar resonant relaxation during which a wire's eccentricity gets to diffuse through resonant coupling between in-plane precessing wires, e.g. precessing because of relativistic effects, (iii) non-resonant relaxation during which a wire's semi-major axis can slowly diffuse under the long-term effects of a series of local Keplerian deflections by nearby stars. A detailed characterisation and implementation of all three dynamical processes will be at the heart of this WP, as will be the link to the existing S cluster at the GC. 
This relaxation process is critical in order to predict the rates of tidal disruptions of stars by MBHs (e.g. Rauch+’96), the merging rates of binary supermassive MBHs (e.g. Yu, 02), or the rate of gravitational wave emissions from star-MBH interactions (e.g. Hopman+’06; Merritt+’11). Resonant relaxation is also the appropriate framework to predict how young stellar populations found in the center of our own Galaxy respond (e.g. Kocsis +’11, Bar-Or+18, and Figure 3) to relativistic effects, in order to quantify the expected rate of infall on the MBH and its spin. One method to study the secular dynamics of quasi-Keplerian stellar clusters will be to rely on direct N−body simulations. We adopt this approach in WPT2 for validation.

However, gaining physical insights from these simulations is challenging, as various complex dynamical processes are intimately entangled there. In addition, because of the significant breadth of timescales between the fast Keplerian motion and cosmic times, the computational costs are such that one can typically only run a few realisations, limited to a relatively small number N of particles. Moreover, this cannot be scaled up easily to astrophysical systems, as different dynamical mechanisms scale differently with N (Heggie+’03). When focusing on resonant relaxation,

WPC2 The black hole - star cluster nexus SEGAL will follow Kocsis+’15 using N−wires code in which stars are replaced by orbit-averaged Keplerian wires for validation. The main approach to understand their dynamics is to rely on kinetic theory (Fouvry+’17). The inhomogeneous Balescu-Lenard formalism is perfectly suited to account for effects induced by the system’s finite number of stars in the cluster. This equation captures the drift and diffusion of particles’ actions induced by their mutual resonant interaction at the frequency shifts induced by relativistic effects and the cluster’s self-gravity. It will be solved directly using FEM. Its SDE counterpart will be implemented at the core of this WP to characterise the individual dynamics of one test wire in this system: on secular timescales, this wire follows a random walk driven by the stochastic Langevin force, which will be computed from the drift and diffusion coefficients of the Fokker Planck and Balescu Lennard equations. The resulting predictions will then be compared to those of the η-formalism, an existing stochastic Fokker-Plank solver (Bar-Or+‘14,17). Self-consistency will be taken care of, while accounting for mass and angular momentum spin-up of the MBH (or binary MBHs). The MBH’s larger-scale fluctuating environment will also be quantified to assess if it impacts the inner cluster’s dynamics and its impact on EMRIs. GRAVITY (Eisenhauer+11) will soon detect the pericenter shift which will allow a new test of general relativity5 and allow to explore the cluster at the scale of the orbit and eventually constrain the spin of Sgr A*. We will specifically consider flat and spherical multi-mass clusters and answer the following questions i) Can we model the stellar mass accretion rate on the MBH? ii) Can the long timescale phenomenology in the vicinity of the so-called Schwarzschild barrier be reproduced by SDE diffusion based on the first principle Balescu-Lenard kinetic equation? iii) Is resonant relaxation between stellar orbits only effective in a restricted region of phase-space away from the last stable orbit lines? iv) Can stochastic solutions produce numerical results consistent with direct N-body results for plunge rates? v) What should be the observed distribution of GR-detected mergers? vi) What drives the interplay between the MBH and its nuclear cluster? vii) what role does the stellar cluster play in spinning Kerr black holes?

Results & Deliverables: Characteristic timescale for each diffusion process; Detailed computations of the relaxation timescales in the whole orbital space surrounding SgrA* for scalar resonant relaxation, vector resonant relaxation, non-resonant relaxation. All shared as a publicly available code. Prediction of the EMRI rate as a function of a stellar cluster's properties (e.g. density power law index and mass spectrum). Computation of the MBH mass and spin growth as sourced by the relaxation of the stellar cluster. Comparison of the statistical distribution of observed stellar properties in SgrA* (e.g. eccentricity or density distribution) w.r.t. the expectations from the relaxation processes. Quantitative estimation of the dissolution time of stellar discs in the vicinity of SgrA* and comparison with the observed discs. Constraints on the efficiency of mass segregation (e.g. between stars and intermediate mass black holes) from observations and theoretical expectations.