Secular Public

Galaxies are unique laboratories to test the universal law of gravity, the driving force from their inner cores to their outskirts. Astronomers have recently focused significant amounts of theoretical, computational and observational efforts to understand and explain their cosmic evolution. This rising interest can be explained by the alignment of three transformational shifts:

1. First, new ground-based or space instruments like Muse, Gravity, MaNGA/SAMI and Gaia are collecting an unprecedented wealth of data probing the long-term dynamical state of galaxies on all scales. We now have access to precision astrometric data on the phase-space structure of our Milky Way (literally billions of stars), complemented by statistical samples of kinetic information on large populations of galaxies;
2. Second, the steady increase in computing power allows us to perform numerical simulations of resolution and complexity greater than ever before in the context of the Cold Dark Matter (CDM) paradigm. Such a framework is now well-established and successfully describes the formation of structures on large scales, but several challenges are still present on the smaller ones. In this respect, the development of progressively more accurate numerical simulations is essential. This applies not only to isolated and idealised setups, but also to account statistically for the fluctuating environment on different scales, from galactic centers to the outskirts of dark halos. These self-gravitating astrophysical systems can therefore now be considered nested, embedded in their own lively environment, with which they interact throughout their lifetime;
3. Finally, recent theoretical breakthroughs in our understanding of the kinetic theory of self-gravitating systems allow us for the first time to follow the effects of gravitationally-amplified external and internal perturbation on the orbital structure of galaxies over cosmic time. In particular, we now have self-consistent integro-differential equations describing the quasi-linear evolution of a given system under the effect of self-induced (e.g. through the system’s own graininess) or externally-driven fluctuations.

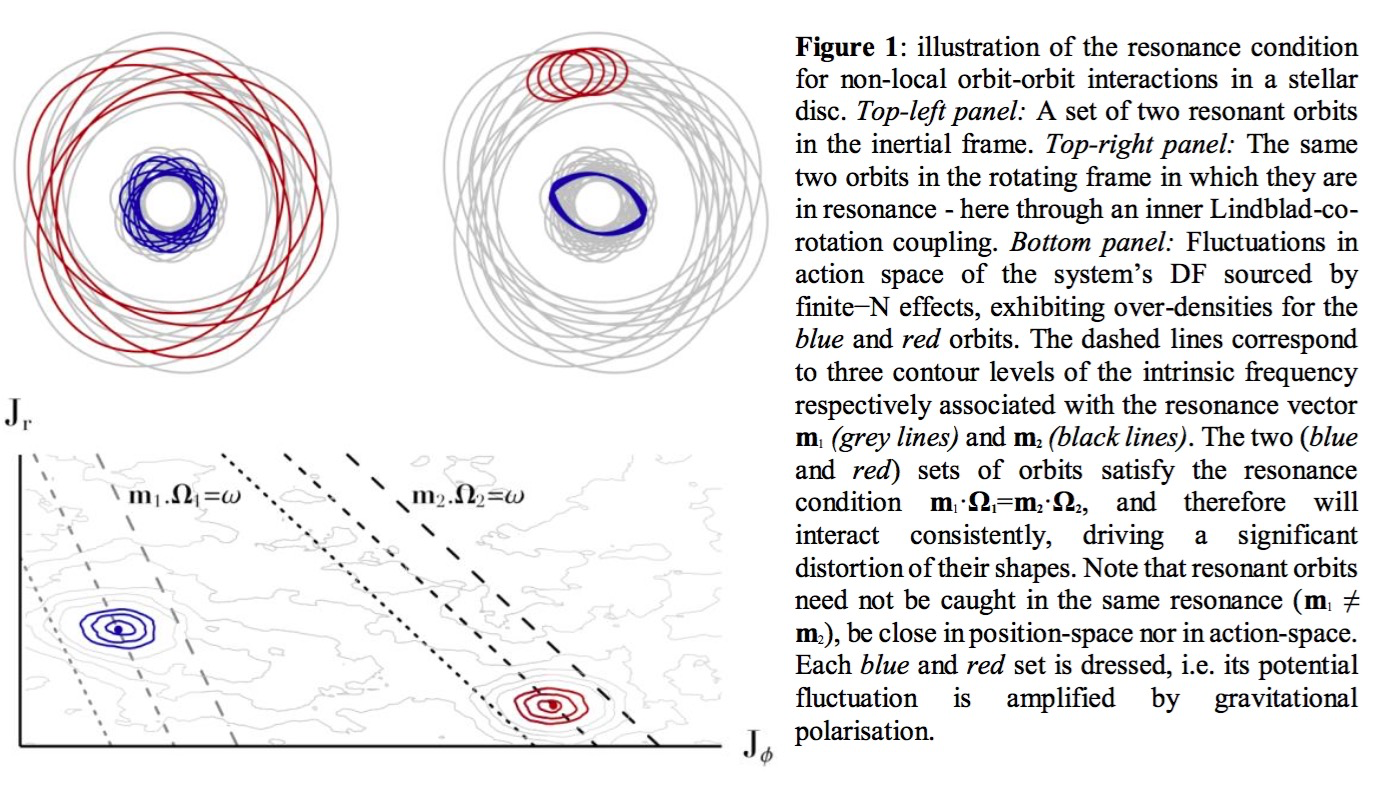
Building upon the seminal works describing the linear response of self-gravitating systems (by Goldreich, Lynden-Bell, Toomre, Kalnajs and others), the development in kinetic theory of a self-consistent framework to characterise their quasi-linear response (Weinberg’01) now offers us a unique opportunity to follow galaxies over cosmic timescales. As for the Earth, galaxies are indeed subject to ‘weather’ and ‘climate’. The former is driven by transients (which reflect recent disturbances which have not yet phase mixed), while the latter encodes distinctive features specifically in orbital space generated over long (secular) timescales. Quasi-linear theory captures the latter. It is, therefore, ideally suited to describe galaxies on large and small scales, because their dynamical times are very short compared to a Hubble time. For galaxies, the most significant (non serendipitous) processes are secular in nature. This motivates the present proposal: through the corresponding stochastic differential equations (SDE), galactic dynamics can now make statistical predictions over cosmic times. The kinetic developments rely on the inhomogeneous Balescu-Lenard (IBL) equation (Heyvaerts’10, and Figure 1 below), i.e. the master equation describing self-induced fluctuations on the one hand, and a proper accounting of environmentally- driven fluctuations and their gravitational amplification, captured by the dressed Fokker-Planck (dFP) equation on the other hand[1]. These equations allow us to gauge the respective roles of nature vs. nurture in establishing the long term observed kinetic properties of galaxies, relying on stochastic processes which capture all sources of fluctuations. The corresponding extended kinetic theories (see e.g. Fouvry+’15,’18 and footnote 1 for a mini review) define a computational framework to quantify statistically the long-term evolution of self-gravitating systems, complementing (commonly used) N-body methods. Qualitatively, these kinetic equations all involve diffusion coefficients in orbital (action) space, Dm(J), scaling like the power spectrum of the dressed potential fluctuations projected along the unperturbed trajectories (with m the harmonic number of the resonance, J the action and Ω the frequencies):

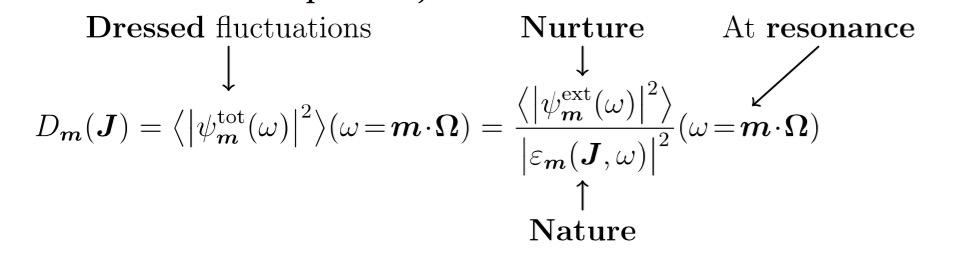
In a stellar/collisionless “fluid”, this diffusion coefficient (which drives the secular distortion of its orbital structure, following the dissipation-fluctuation theorem) is amplified by the square of its inverse gravitational susceptibility, ε, evaluated at the natural frequencies of the system. If the perturbation hits these natural frequencies while the system is not far from marginal stability, anisotropic diffusion along that resonance can be extremely efficient and cause rapid changes. Whether they are external or self-induced, the long-term resonant effects of potential perturbations on galaxies can therefore now be accounted for in detail, by quantifying their spectral properties on small (central cluster), intermediate (disc) and large (halo, globular cluster system) scales. This distinction between processes specific to each scale is made possible by the chosen dichotomy between external and internal fluctuations. It is a requirement to capture secularly the many scales involved.

The distinction also allows us to disentangle their respective roles in sourcing secular evolution, as we quantify the diffusion signatures and the characteristic timescales associated with each source of fluctuations. For instance, in stellar discs, we must investigate the relative diffusive efficiency of shot noise triggered by Giant Molecular Clouds (GMCs), clumps within the halo, central bars, etc. We must also quantify external sources of fluctuations: flybys, infall etc. We must finally pay attention to the system’s initial reservoir of free energy, which differs greatly between, e.g. spirals and ellipticals, and to the secular transformation of the underlying equilibria through infall. Once all these mechanisms are statistically characterised and quantified, long-term implications (e.g. for the age-dispersion relations within discs, the impact of bars) can be compared to detailed observations, e.g. of the structure of the Milky Way’s distribution function (DF), provided by Gaia (e.g. through structures in the U-V plane). The system’s DF may involve additional parameters (in so-called extended phase space), such as stellar metallicity, which traces the interplay between dynamics and chemistry (abundances, alpha-enhanced elements, etc, which are indirect proxies for stellar age). Hence one also needs to account for cold gas inflow and the birth (and possibly death) of stars, i.e. for the possibility of sources and sinks of particles. We must finally follow multiple masses and describe the corresponding secularly induced mass segregation. This is essential near the Galaxy’s massive black hole (MBH), but more generally of interest in the context of stellar discs, and even galactic halos, where substructures within the halo act as an effective varying number of massive quasi-particles. All these scales have in common that gravity and resonances drive their secular evolution. Hence a novel single framework can explain the long-term behaviour of various components of galaxies, seemingly different as they involve nested scales, but in reality, describable through the same approach. SEGAL will quantify the cosmic fate of these self-gravitating systems over a Hubble time and identify asymptotic solutions, specific to each scale. SEGAL will study the statistical impact of e.g. stellar migration, disc thickening via giant molecular clouds and spiral waves, resonant relaxation in galactic centers, bars and globular clusters, or the reshuffling of the orbital structure of dark halo cores. This is both unprecedented and extremely useful.

Building up on the practical advantage of quasi-linear theories capturing the long-term effect of self-gravity in an open multi-scale environment, we must proceed via the following computationally-demanding steps:

• B.1: quantify the environmental effects induced by the larger scale using ensemble of simulations; compute the relevant power spectra driving externally induced fluctuations at each scale; 

• B.2: implement both secular formalisms, solving for the joint kinetic equations and quantifying each characteristic timescale, while accounting for the difference in temperature and degeneracies specific to each scale; identify the generic asymptotic solutions (resp. core halos, exponential discs, cusps...);
• B.3: cast our results in terms of observables, tailored to existing and future facilities, and propose new observational diagnostics to test our theoretical predictions. 


B.1 Quantifying the fluctuating environment: We will rely on SEGAL’s computing resources to produce sets of simulations to account statistically for the specific fluctuating environment on the boundary of that scale, from galactic centers to the outskirts of dark halos, so that the inner boundary of each outer-scale corresponds to the environment of its inner-scale. The assumption will be that while the detailed long-term results of N-body or hydrodynamical simulations should be considered with the appropriate level of skepticism, their short-term ensemble-averaged behaviour on the larger scales are more robust. Within SEGAL we will focus only on canonical angular power spectra (involving the Fourier transform of the potential fluctuations w.r.t. the angle coordinates conjugated to the actions – labeling orbits), since the fluctuation-dissipation theorem tells us they are the relevant quantity. We will use multi-scale, zoomed-in simulations that include massive black holes, stellar and AGN feedback in the spirit of New-Horizon. We pioneered such measurements using over 15 000 dark halos at the Virial radius in Aubert+’07, over 50,000 and 200,000 virtual galaxies, in Pichon+’11 and Dubois+’14. The fluctuation dissipation theorem provides us with a shortcut: from the point of view of the underlying orbital structure, only the power spectrum of fluctuations matters. This is a significant compression of the full statistics! We will rely on zoom on multiple resolutions in order to fit and extrapolate these power spectra. These fits will be deliverables of the project and made available to the community. We will also compute explicitly the ensemble average over sets of galaxies of the rate of change of actions which enter the quasi-linear diffusion equations as fluxes.

B.2 Solving for the kinetic equations: Most of the existing published works on self-gravitating kinetic theory, with the noticeable exception of Weinberg’s’01 paper, were restricted to computing the initial diffusion flux of the extended kinetic equations. In order to probe later stages of secular evolution, SEGAL must integrate forward in time secular diffusion equations. There are a few anticipated (significant) difficulties. The first arises from the self-consistency of the diffusion equations. Since the response matrix encapsulates the self-gravity of the system, it intrinsically involves a double integration over phase-space. The system’s drift and diffusion coefficients depend on the current global value of the system’s DF and have to be updated as the system evolves. For the inhomogeneous Balescu-Lenard equation, the dependency is explicit and quadratic, and implicit via the response matrix. For the explicitly linear Fokker Planck equation, there is again implicit dependency via the response matrix. The integration in time has to be made step-by-step, with successive updates of the system’s DF, potential, and diffusion flux. Integrating such a partial differential equation is a challenging numerical calculation, which can involve complex finite elements methods (FEM). As a validation, one of the work packages of SEGAL will perform this. A preferred alternative package, inspired from Monte Carlo simulations, follows from the Langevin rewriting of the diffusion equation and will be applied to all considered scales (halo, disc, black hole). One samples the system’s DF with individual particles and integrates the first-order stochastic ordinary differential equations (SDE) describing the dynamics of such test orbits. With this formulation, the involved timesteps are commensurable with a fraction of a Hubble time. After a few timesteps, the DF is resampled using cloud-in-cell, and the new matrix response, drift and diffusion coefficients are computed. Some regularisation must be imposed on the estimated (noisy) DF since the matrix and the coefficients involve derivatives of this distribution. Finally, one must take into account possible changes in the DF induced by infall[2].

Such schemes for computing orbital diffusion will also be used to validate the accuracy and robustness of N−body codes on secular timescales. SEGAL will obtain the first hard evidence for the accuracy of numerical integrators over Hubble times and various scales.[3] Asymptotic solutions to the kinetic equation should correspond to the observed quasi-stationary states of the corresponding secular process, given final mitigations between environmental and intrinsic effects. The end result of this step will be the full knowledge of DF(J,τ).

B.3 Compute observables for upcoming surveys: Today, the synergy of telescopes and spacecrafts at different wavelengths allows us to study galaxies, and embedded MBHs at unprecedented resolution. Gaia, MANGA, SAMI, the VLT with Gravity, are all online and fully working. On longer timescales, following the first detection of gravitational waves by LIGO in 2015, upcoming instruments like LISA will measure the rate at which massive black holes in galactic centers swallow stars and spin up. JWST, DESI, LSST, Euclid, 4MOST, and MOONS will soon provide a comprehensive view of galaxies and their MBH hosts. All our results (the DFs) must therefore be cast in terms of direct observables, tailored to these existing and future facilities, in order to interpret such datasets. These observables are typically marginals of the underlying DF(J,τ) and are therefore ‘straightforwardly’ computed. For instance, the so-called Hercules streams in Hipparcos and Gaia data are likely to be kinematic moments of this secular distribution function. Depending on scale, the signatures of our stochastic solutions will be quantified in terms of the evolution of the age-dispersion relations in the Milky Way’s disc, its vertical gradient, and the stellar dynamical evolution of the Galactic center’s cluster (as a probe of e.g. black hole spin). It will also be applied on larger scales to investigate the cusp-core problem of dark matter, the persistence of streams within dark halos.

Understanding the long-term evolution of the components of galaxies such as stellar discs and galactic centers is now a subject of intensive research. In this context, the purpose of SEGAL is to establish quasi-linear theory as an ideal tool and enlightening addition to N-body simulations to probe statistically the cosmic fate of galaxies on multiple scales over a good fraction of a Hubble time. With the present public release of the GAIA data, a detailed theoretical modelling of the-long term evolution of the Milky Way’s internal structure is in order. Quasi-linear theory is for instance ideally suited to explain the novel observed features in the phase-space of our Milky Way. The cross-validation of N-body simulations via kinetic theory on secular timescales is now also of prime importance for upcoming projects like DESI, LSST, Euclid, 4MOST, MOONS etc, which rely heavily on modeling the dynamics of galaxies to mock their surveys. Eventually we will be able to gauge the roles of nature vs. nurture in establishing the observed properties of galaxy population on small and large scales, something currently out of reach of standard N-body techniques. Finally, the universal nature of gravitational kinetic theory could eventually allow us to address related problems, such as the secular evolution of proto-planetary discs. More generally, gravity, with its rich phenomenology, is ideally suited to help us understand in detail the secular implications of collective modes, shot noise and resonances. As such, it will continue to enlighten our understanding of the underlying mathematics, capturing fundamental physical processes such as entropy production, anisotropic resonant diffusion, secular phase transition etc. Hence gravitational kinetic theory will also stimulate progress and innovative research in theoretical physics and beyond. In essence, this area of research will, therefore, thrive in the coming years, as the communities active in cosmology and formation and dynamics of galaxies and star clusters are already converging towards a common set of open questions and challenges, and have much to learn from one another. SEGAL has the ambition to tackle exactly this - mostly unexplored - scientific intersection. Such a spirit, coupled with the novelty of the proposed methodology, generates great potential for discovery. The ultimate outcome of this unique synergy will be a deeper understanding of the fundamental physical processes in the assembly of cosmic structures in our universe and the proposed programme will contribute significantly to this endeavour.