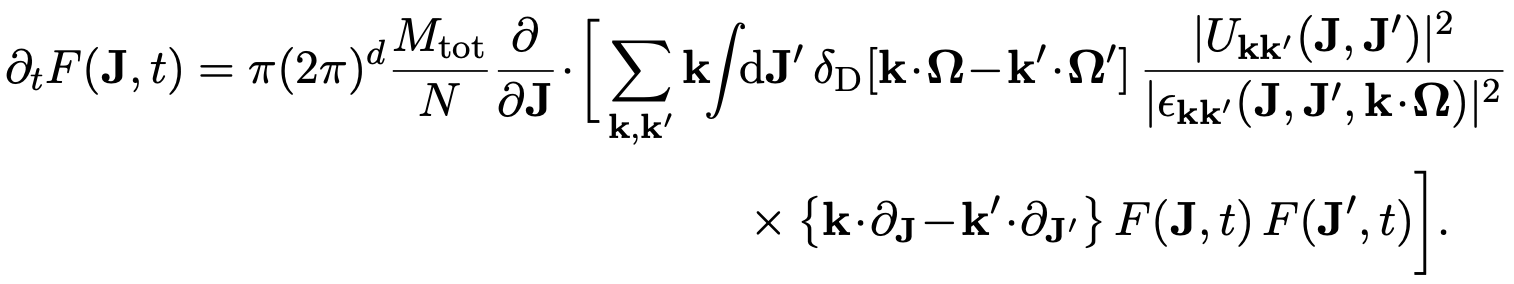Secular Public

Astrophysical Context

Self-gravitating systems are ubiquitous in the Universe. They can be hierarchical like galactic nuclei or dynamically degenerate like harmonic cores in the centre of galaxies. They can be dynamically cold like galactic discs or dynamically hot like globular clusters. Any worthy attempt at describing the long-term evolution of these self-gravitating systems must necessarily account for all these defining features, as they fundamentally imprint the details of their long-term behaviour. Capturing the dynamics driven by self-generated perturbations from the finite number of stars is what the (inhomogeneous) Balescu-Lenard equation [1] has fairly recently been able to encompass.

The BL equation is the key fundamental master equation to describe the self-induced resonant long-term amplified relaxation of stellar clusters. Its strength lies in its generality and physical richness. For example, BL accounts for global inhomogeneity (i.e. intricate stellar orbits), linear amplification (i.e. collective gravitational dressing), non-local resonances (i.e. long-range stellar encounters), diffusion and friction (i.e. dynamical heating and cooling in galaxies), and irreversibility (i.e. entropy growth). Owing to its versatility, BL applies to systems as varied as galactic discs [2], galactic nuclei [3] or globular clusters [4]. In each of these contexts, BL has recently shown its effectiveness to describe quantitatively challenging regimes of dynamical relaxation.

Yet, this kinetic formalism builds upon some stringent assumptions. These prohibit more generic applications. In particular, BL relies on (i) a quasilinear assumption (perturbations must be small); (ii) an ensemble average (BL only describes the “average” galaxy); (iii) a weak collective amplification (self-gravitating amplification must be small); (iv) a smooth interaction potential (stellar orbits must be quasiperiodic). Lifting these assumptions is a mandatory step to further generalise BL and make it an ever more efficient statistical framework to devise long-term kinetic theories in self-gravitating systems.

Upshot

This is where the heart of the present PhD project lies. Its goal is to expand and generalise the BL equation by lifting some of the key assumptions on which it lies. In particular, the PhD candidate will focus on precisely quantifying the impact of non-linear effects, stochastic contributions, resonances and chaotic diffusion in the context of long-term astrophysical relaxations. Once completed, this PhD project will have highlighted the predictive power of statistical methods stemming from kinetic theory to describe the intricate evolution of stellar systems.

Objectives

• Non-linear saturation. In the presence of large fluctuations, e.g., a galactic disc with a growing spiral arm [5], BL’s underlying quasilinear assumption fails. Taking inspiration from renormalisation theory [6], the PhD candidate will estimate, for the first time, the non-linear response function of galaxies to predict the final level of out-of-equilibrium features. How important is the quenching of amplification by non-linear effects?
• Long-term stochasticity. In the presence of long-lived perturbations, e.g., a sloshing mode in a globular cluster, stochasticity can pop up on long timescales, an effect that BL misses. Revisiting the ansatz of timescale separation [7], the PhD candidate will unveil the dynamical origin of the long-term dispersion among seemingly identical stellar systems. How large is the scatter in the time of bar formation between different disc galaxies?
• Fundamental degeneracies. In harmonic cores [8], all stellar orbits share the exact same orbital frequencies. This makes BL’s resonance condition intrinsically ill-defined. Using an appropriate time-averaged Hamiltonian, the PhD candidate will describe long-term relaxation in over-resonant systems. Can this explain the apparent stalling of dynamical friction in the centre of dwarf galaxies [9]?
• Beyond integrability. The BL equation assumes integrability, i.e. the existence of angle-action coordinates, for example through global symmetries [10]. Lifting this assumption, the PhD candidate will investigate non-integrable systems, e.g., thickened galactic discs [11] to characterise stochastic diffusion in the presence of partial chaos. Is stellar diffusion accelerated in triaxial galaxies compared to razor-thin ones?

Requirement

Strong interest in theoretical astronomy, dynamics, analytical and numerical work.

Framework

PhD supervised by Jean-Baptiste Fouvry at the Institut d'Astrophysique de Paris.

References

[1] Heyvaerts, 2010, MNRAS, 407, 355
[2] Fouvry+, 2015, A&A, 584, A129
[3] Fouvry+, 2021, MNRAS, 508, 2210
[4] Bar-Or+, 2018, ApJL, 860, L23
[5] Hamilton, 2023, MNRAS, 528, 5286
[6] Krommes+, 1979, Phys. Fluids, 22, 2168
[7] Chavanis, 2012, Physica A, 391, 3680
[8] Sellwood, 2015, MNRAS, 453, 2919
[9] Read+, 2006, MNRAS, 373, 1451
[10] Binney & Tremaine, 2008, Galactic Dynamics
[11] Fouvry+, 2017, MNRAS, 471, 2642